Les programmes officiels de CE1 et CE2 en mathématiques sont très proches. Ils peuvent être travaillé sur plusieurs aspects via les briques LEGO® DUPLO®.
📘 Le programme de CE1 et CE2 (cycle 2):
En CE1, l’enfant apprend à dénombrer, constituer et comparer des collections jusqu’à 99. En CE2, cette compétence s’étend jusqu’à 999. Il s’agit de savoir compter des objets et de reconnaître les nombres à travers différentes représentations.
Les élèves apprennent également à comparer, ranger, encadrer et intercaler des nombres entiers. Pour cela, ils utilisent les symboles mathématiques >, < et =, qui leur permettent de situer les nombres les uns par rapport aux autres.
Le nombre peut être présenté de plusieurs manières : en chiffres, en lettres, sous forme de constellations, de points sur des dés, de doigts levés, ou encore sur une règle graduée. Cette diversité de représentations aide l’enfant à faire le lien entre le concret et l’abstrait.
Les enfants en Cycle 2 commencent à résoudre des problèmes en mobilisant les opérations d’addition et de soustraction, pour donner du sens aux situations de la vie quotidienne.
📎En savoir plus :
- https://eduscol.education.fr/84/j-enseigne-au-cycle-2
- https://www.education.gouv.fr/programmes-et-horaires-l-ecole-elementaire-9011
- https://www.education.gouv.fr/sites/default/files/ensel135_annexe4.pdf
- 2021_guide_mathematiques_cp
📖 Exemples d’utilisation de briques et de dés
Toutes ces notions mathématiques peuvent être abordées avec des briques et des dés.
Les nombres jusqu’à 99 (CE1) et 999 (CE2)

Pour créer aléatoirement un nombre allant de 0 à 999, nous pouvons utiliser des dés à 10 faces numérotés de 0 à 9. Chaque dé représente l’Unité, la Dizaine, la Centaine. L’exercice peut être adapté selon le niveau de l’enfant avec l’utilisation d’un ou de 2 dés uniquement.
A chaque valeur de dé est associée une couleur. Ainsi, les briques « Unité » se comptent de 1 en 1, les briques « Dizaine » de 10 en 10 et les « Centaine » de 100 en 100. Nous pourrions également utiliser des pièces et des billets factices pour illustrer l’exemple.
Cet exercice demande un peu de matériel (dés à 10 faces et briques de couleurs) mais tout est réutilisable.
Pour les valeurs inscrites sur les briques nous utiliserons des feutres à tableau blanc (donc effaçable!).
La comparaison de nombres
L’utilisation de dés est une nouvelle manière de créer des nombres aléatoires et casser le rythme des « comptines » de chiffres.
Dans le 1er cas, nous allons utiliser 2 dés à 6 faces avec des constellations de points. Il faudra reconnaitre le bon chiffre et y associer la brique « chiffre ». Puis, la construction de 2 tours pour mesurer la tour la plus haute.
Dans le second cas, l’utilisation de dés à 10 faces allant de 1 à 10 permet d’obtenir plus de combinaisons et varier la lecture des chiffres.
Dans le 3ème cas, nous pourrons utiliser plusieurs chiffres avec des dès à 10 faces (0 à 9) pour construire des nombres. Un règle sera mise en place pour définir l’unité et la dizaine: 1er dé lancé = unité, 2ème dé = dizsaine.
Les représentations du nombre
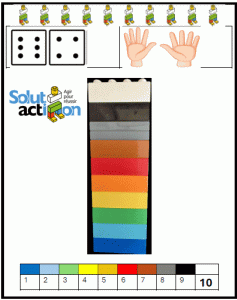
Un nombre peut être représenté de plusieurs manières. Dans notre carte exemple, 10 est représenté par une constellation de 10 logos, la somme de 2 dés, les doigts de la main, une règle de couleur et une tour de briques de couleurs. D’autres représentations sont envisageables.
La résolution de problème par des additions ou soustractions
Ces exercices deviennent concrets en manipulant des objets, comme les briques.

Un exemple:
- Tu as 2 briques. Je t’en donne 3 en plus. Combien as-tu de briques en tout?
- Tu as 2 briques. Combien dois-je te donner de briques supplémentaires pour en avoir 5 ?
🧱 Pourquoi utiliser des objets à manipuler pour les mathématiques CE 1 et CE 2?
À l’âge du CE1 et du CE2, les enfants construisent leurs apprentissages à travers l’expérience concrète. Avant de pouvoir raisonner de manière abstraite, ils ont besoin de voir, toucher et manipuler. Les briques LEGO® et DUPLO® deviennent alors un formidable support pour donner vie aux notions scolaires.
En mathématiques, par exemple, il est souvent difficile pour un enfant d’imaginer une dizaine, une centaine ou encore une fraction. Les briques permettent de rendre visible ce qui est invisible :
- Une tour de dix briques devient une dizaine.
- Une plaque peut représenter l’unité de base pour les centaines.
- Une brique divisée en deux ou en quatre montre concrètement ce qu’est une fraction.
Cette approche s’inscrit directement dans l’esprit de la méthode de Singapour.
Ainsi, un enfant comprend d’abord par l’action, puis par l’image, avant de pouvoir raisonner uniquement avec des nombres. Cette progression est particulièrement bénéfique pour les enfants avec des troubles spécifiques de l’apprentissage, comme la dyscalculie ou le trouble du déficit de l’attention, car elle offre une voie alternative et multisensorielle d’accès aux savoirs.
En manipulant, l’enfant se concentre, explore, expérimente et retient mieux. Il prend plaisir à apprendre, car le jeu vient soutenir l’effort scolaire. Les enseignants, parents et aidants y trouvent un outil simple, efficace et motivant pour accompagner les apprentissages, tout en respectant le rythme et les besoins de chaque enfant.


